Gorgias is a press-your-luck dice game of philosophical debates for 2 players.
You'll need the following materials to play Gorgias:
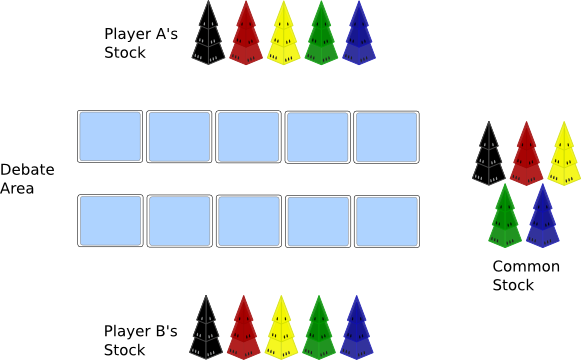
Each player receives a single rainbow set and the third is placed between them and considered a common set. The playing cards are placed face-down in two rows of five where each card is adjacent to one other card.

Once the play area is setup the game can begin.
In any good philosophical debate there are three critical topics of discussion:
In Gorgias it is your task to participate in a philosophical debate that covers, preferably in equal parts, the three core topics. These topics are abstractly represented as symbols on a special pyramid die, or as the first three numbers on a regular die:
| Topic | Pyramid | Die |
|---|---|---|
| Knowledge |  |
 |
| Conduct |  |
 |
| Governance |  |
 |
Any constructed argument must have at least one each of the three core argument topics. However, there are other ways to cover these topics without focusing solely on them by the way of nuanced arguments.
Nuanced arguments feature combined aspects of the core arguments and are represented as faces on a pyramid or regular die:
| Pyramid | Die |
|---|---|
 |
 |
 |
 |
 |
 |
Nuanced arguments are a good way to ensure a powerful case and meet the demands of the three core arguments.
A game of Gorgias consists of eight rounds, or statements, that consist of five groups of pyramids representing the results of rolling the arguments dice. These groups are secretly arranged behind a shield across from the opponent's groups. Once both players' groups are revealed the results are calculated and won pyramids dispersed.
Statements are built by rolling the arguments dice up to three times and keeping any number of dice aside during each roll to formulate the set. However, the lone caveat in building a set is that each of the three core arguments must be represented either as their exact faces or within nuanced arguments.
Whenever a set is rolled without representation in all three core arguments then a die of the arguing player's choice will be removed from play for that round.
Finally, once a set is formed via the pyramid dice rolls then the players pull pyramids from a their personal stock of any color of the size needed to fulfill the pyramids shown on the faces of the dice. Once chosen, the debate can begin.
The results of the dice describe five groups of pyramids that will be aligned with the opponent's five groups, each group on a single playing card. Any individual group will consist of a single pyramid or two pyramids. The pyramid in a group of one can be arranged with its point facing the opposing group or its bottom facing. When the point of the pyramid faces the opponent's group it projects the value of its pips. When it faces away from the opponent's group it absorbs the value of its pips. In a group containing two pyramids one must face the opponent's group and the other must face away.
Before a debate begins the players place a shield between their play areas and secretly arrange their groups in a row. Once arranged the players reveal their layouts and calculate the argument resolutions.
For example:

The pyramids above are oriented in such a way that the left-side group projects 3-points toward the right-side group and absorbs two points. When resolving an argument it's assumed that everything happens at once. Therefore, in the debate above the red pyramid projects 3-points, 2 of which are absorbed by the blue. Since blue only takes 2 of the 3 points, 1 additional flows through to the yellow, thus reducing it by 1. At the same time the yellow pyramid projects 3-points, but since there is no rebuttal the red is completely overwhelmed, leaving no points remaining. At the end of the debate, the right-hand player retains a medium yellow.

For that group a yellow medium pyramid is set aside from the common stock for final scoring. The remaining groups are resolved similarly. After 7 rounds the debate ends and the final scores are tallied.
Every individual pyramid captured will score 1 debate point. However, certain combinations can combine to score more points:
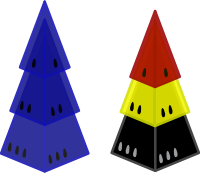
Any combination of three differently sized pyramids will form either a solid-color tree or a multi-color tree. Trees score more points than individual pyramids:
Whomever has the most points wins the debate.
Gorgias is ©2014, Michael Fogus